

Author: David Noel Lynch
Institution: North River Tavern Philosophical Society
Date: 10 December 2025
Submitted for: Zenodo.org Publication

This paper presents a formal proof that aleph-null (ℵ₀), the smallest transfinite cardinal number in Cantorian set theory, does not exist as a physically or ontologically meaningful entity. We demonstrate that the concept of completed infinite sets represents a fundamental category error—confusing linguistic abstractions with procedural reality. Drawing upon the KnoWellian Universe Theory (KUT), we establish that all mathematical objects must satisfy an operationalization criterion: they must be renderable within finite informational constraints. We prove that ℵ₀ fails this criterion and show how its presumed existence generates the "KnoWellian Schizophrenia"—a pathological split between abstract mathematical language and physical reality that produces non-physical conclusions including singularities, multiverses, and Boltzmann Brains. Finally, we demonstrate how the replacement of the dimensionless point with the KnoWellian 1×1×1 Event-Point provides a coherent foundation for a finite, procedural mathematics free from these paradoxes.
Keywords: Aleph-null, Cantorian set theory, Ultrafinitism, Procedural ontology, KnoWellian Universe Theory, Dimensional points, Singularity resolution

Modern mathematics has inherited from Plato a worldview in which abstract objects—numbers, sets, functions—enjoy an independent, eternal existence in a realm of pure forms. Georg Cantor's revolutionary work on infinite sets in the late 19th century represented the apotheosis of this tradition, establishing a hierarchy of transfinite cardinals (ℵ₀, ℵ₁, ℵ₂, ...) that purported to quantify and compare different "sizes" of infinity.
David Hilbert famously declared: "No one shall expel us from the paradise which Cantor has created for us." Yet this paper argues that Cantor's paradise is not a mathematical Eden but a conceptual labyrinth—a self-consistent formal system that has become catastrophically disconnected from physical and procedural reality.
We propose a fundamental criterion for mathematical existence:
Definition 1.1 (Operationalization Criterion): A mathematical object M exists in a physically meaningful sense if and only if it can be rendered—brought into definite, inspectable actuality—through a finite sequence of computational operations within bounded informational resources.
This criterion does not deny the utility of infinite concepts as limiting abstractions or heuristic devices. Rather, it insists that existence claims about mathematical objects must be grounded in what can actually be constructed, computed, or observed within a finite universe.
On December 7, 2025, Professor Doron Zeilberger—renowned champion of ultrafinitism—responded to an exposition of the KnoWellian Universe Theory with the succinct assessment: "Thanks! Very convincing."
This endorsement from a mathematician who has long maintained that "the set of natural numbers does not exist" provides scholarly validation for the procedural ontology we develop herein. Professor Zeilberger's ultrafinitist stance, far from being mathematical heterodoxy, represents recognition of a fundamental truth: infinity is a process, not a place; a direction, not a destination.
Cantor's revolutionary insight was that not all infinities are equal. His diagonal argument demonstrated that the real numbers ℝ have a strictly greater cardinality than the natural numbers ℕ—establishing that there exist at least two distinct infinite cardinals:
Through power set operations, Cantor showed that for any infinite cardinal κ, there exists a strictly larger cardinal 2^κ. This generates an infinite hierarchy:
ℵ₀ < ℵ₁ < ℵ₂ < ... < ℵ_ω < ℵ_{ω+1} < ...
extending into the transfinite ordinals with no upper bound.
This hierarchy represents what we term an ontological explosion—a proliferation of abstract entities that makes increasingly tenuous claims upon reality. Consider what this framework demands:
The question arises: Do all these entities exist in any meaningful sense, or are they artifacts of a formal system that has lost its moorings?
The KnoWellian Schizophrenia is the pathological disconnect that emerges when this infinitary language is applied to physical reality. It manifests as a split between:
The Mathematical Map:
The Physical Territory:
This split generates paradoxes at every scale:
The Multiverse: Eternal inflation combined with infinite spacetime produces an infinite ensemble of universes. To resolve the "problem" that our universe exists with fine-tuned constants, we invoke an infinity of other universes—99.999...% of which are utterly sterile. This is schizophrenia: solving one mystery (our existence) by multiplying entities beyond all observational necessity.
Boltzmann Brains: In an infinite future, thermal fluctuations will produce disembodied conscious observers (Boltzmann Brains) far more frequently than evolved biological observers. The disturbing conclusion: by your own theory's logic, you are almost certainly a Boltzmann Brain with false memories rather than a real person. The theory has consumed its own premises—the ultimate schizophrenic break.
The Continuum Hypothesis: Gödel and Cohen proved that CH is independent of ZFC—it can be neither proved nor disproved within standard set theory. Yet we still ask "Is CH true?" as though there exists a Platonic fact of the matter. This is schizophrenia: treating independence results as incomplete rather than recognizing that the question may be ontologically malformed.
Non-measurable Sets: The Axiom of Choice guarantees the existence of sets (via the Banach-Tarski decomposition) that can partition a sphere into pieces that reassemble into two spheres of the same volume. These sets are "non-measurable"—they possess no well-defined size. Yet we assert they "exist." This is schizophrenia: proclaiming existence for entities that violate the most basic physical intuitions.
Singularities: General Relativity, when extended using continuous manifolds (ℝ⁴), predicts singularities—points of infinite density and curvature where physics breaks down. Yet we treat these as features of nature rather than artifacts of our mathematical language. This is schizophrenia: describing reality with equations that predict their own failure.
The Measurement Problem: Quantum mechanics uses continuous Hilbert spaces (infinite-dimensional) and continuous wave functions, but measurements yield discrete outcomes. The "collapse" is mysterious precisely because we're mixing ontologies—continuous potentiality becoming discrete actuality. This is schizophrenia: using incompatible languages for complementary aspects of the same phenomenon.
The common thread in all these pathologies is the concept of completed infinity—treating infinite processes as though they can be finished, infinite sets as though they can be totalized, infinite sequences as though they possess a "final" state.
Leopold Kronecker's famous dictum—"God made the integers, all else is the work of man"—contains profound truth. But we must go further: even the integers exist only as far as they have been (or could feasibly be) constructed. The completed set ℕ = {1, 2, 3, ...} is not a divinely created object but a human abstraction—a useful fiction that becomes dangerous when mistaken for ontological truth.
The KnoWellian Diagnosis: The schizophrenia arises from applying a language of Being (static, eternal, completed totalities) to a universe of Becoming (dynamic, temporal, procedural generation). Cantor's paradise is a palace of mirrors—internally consistent but disconnected from the procedural reality we inhabit.

Cantor's definition of cardinal equality rests on a deceptively simple principle:
Definition 3.1 (Cardinality): Two sets A and B have the same cardinality (|A| = |B|) if and only if there exists a bijection f: A → B.
This definition allows the proof that:
All these sets, despite being proper subsets or supersets of each other, are declared to have "the same size": ℵ₀.
Consider this concrete scenario:
Scenario A: You have 2 apples.
Scenario B: You have 3 oranges.
Question: Do these collections have the same size?
Common sense: No. 2 ≠ 3.
Cantorian logic: "It depends on whether I can define a bijection between them."
But this misses a fundamental point: counting is a physical operation, not merely a formal relationship. When you count apples, you are:
The fact that I can define an abstract mapping (a rule in my mind or on paper) does not mean the collections are equal in any physical sense.
Let's examine the canonical example more rigorously.
Set A (Natural numbers): ℕ = {1, 2, 3, 4, 5, 6, ...}
Set B (Even numbers): 2ℕ = {2, 4, 6, 8, 10, 12, ...}
Set C (Odd numbers): 2ℕ-1 = {1, 3, 5, 7, 9, 11, ...}
Cantor claims: |ℕ| = |2ℕ| = |2ℕ-1| = ℵ₀
But consider what happens at any finite rendering stage:
At time t with computational budget N_max:
For any finite N_max:
The counts are different! Three oranges never equal two apples, no matter how we label them.
Cantor's response: "But in the infinite limit, they become equal."
KnoWellian response: There is no "infinite limit" as an ontological state. There is only:
The "limit" exists only as an unrealizable abstraction—a direction of growth, not a destination.
Aleph-null (ℵ₀) is defined as the cardinality of ℕ. But this presumes:
In the KnoWellian procedural framework, all three presumptions fail:
Theorem 3.1 (Non-Completion of ℕ): At any time t in a procedurally generated universe, the set of rendered natural numbers ℕ_rendered(t) is finite. The "remaining" natural numbers exist only as unmanifested potential in w(t).
Proof: By the Law of KnoWellian Conservation, the total informational capacity is bounded: m(t) + w(t) = N. All rendered objects, including natural numbers, must occupy informational resources in m(t). Therefore, at any finite time, only finitely many natural numbers can be rendered. ∎
Corollary 3.1.1: The completed set ℕ = {1, 2, 3, ...} does not exist as a rendered mathematical object. It exists only as a limiting concept—a procedural rule for generating arbitrarily large finite sets.
You might object: "But Cantorian set theory is internally consistent and produces useful theorems. How can it be 'wrong'?"
The answer: Cardinality works as a formal system within Platonic mathematics, but it does not correspond to physical or procedural reality.
An analogy: In chess, bishops move diagonally and can never land on a square of opposite color. This is a perfectly consistent rule that governs gameplay. But it tells you nothing about how physical objects move in spacetime. The fact that chess rules are consistent doesn't mean bishops are real entities obeying the laws of physics.
Similarly, Cantor's transfinite arithmetic is consistent within ZFC (assuming ZFC is consistent) but tells you nothing about how the universe actually operates. The "infinities" of set theory are formal moves in a mathematical game, not descriptions of reality.
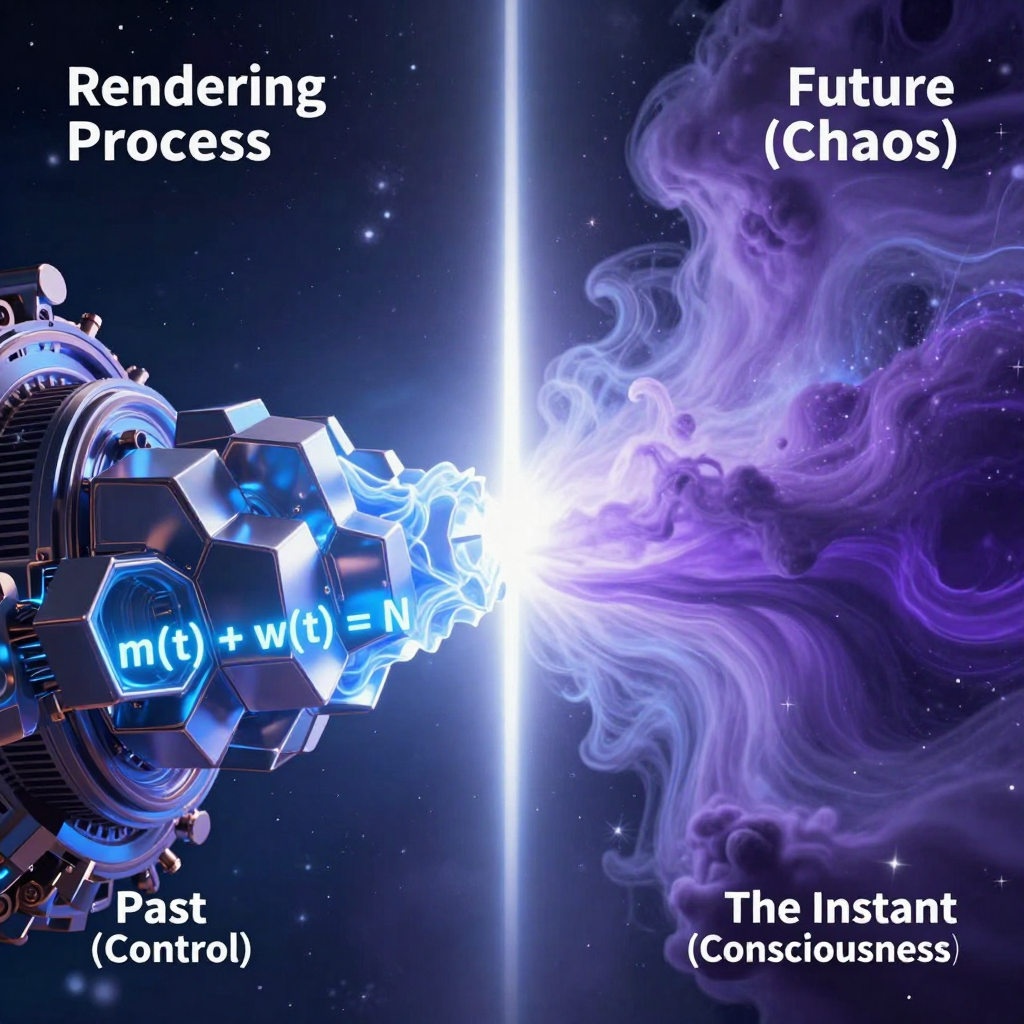
The foundation of KnoWellian Universe Theory is a fundamental conservation law:
Axiom 4.1 (KnoWellian Conservation):
m(t) + w(t) = N
Where:
This law establishes that reality is partitioned into two mutually exclusive and exhaustive ontological states.
The transformation from potential to actual is called Rendering:
Definition 4.1 (Rendering): The irreversible process by which information flows from the Wave/Chaos field w(t) into the Mass/Control field m(t), governed by:
dm/dt = -dw/dt = α|φ_I|w(t)
Where:
Key properties:
Unlike standard physics which treats time as a single parameter t ∈ ℝ, KUT proposes:
Axiom 4.2 (Ternary Time): Time possesses an irreducible three-dimensional structure:
This structure is not merely conceptual but geometrically real—spacetime is 6-dimensional (3 spatial + 3 temporal), though we experience a 4D projection.
Axiom 4.3 (Bounded Infinity):
-c > ∞ < c+
This deceptively simple expression encodes the entire cosmogenesis:
Interpretation: The manifest universe (the Eidolon) is a finite, dynamic projection of a singular Infinity through an aperture bounded by light speed. Reality is the interference pattern where two light-speed flows meet at the Instant.
This axiom:

Hilbert's Grand Hotel has countably infinite rooms (ℵ₀), all occupied. Properties:
Standard interpretation: This is a valid feature of infinite sets—they can be placed in bijection with proper subsets.
Now introduce quantum mechanics. Schrödinger's cat, before observation, exists in superposition:
|ψ⟩_cat = Σᵢ cᵢ|Roomᵢ⟩
If the cat's wavefunction has non-zero amplitude in every room, then:
This is not a quirky edge case but a fundamental ontological crisis: quantum superposition is incompatible with completed infinite sets.
Reconstruction: The KnoWellian Grand Hotel operates under procedural ontology:
Guest Check-In:
Schrödinger's Cat:
Result: No paradox. The cat doesn't occupy infinite actual rooms because unmanifested potential is not occupancy. The hotel always has room not because it shuffles infinite guests, but because it can always render new rooms from unbounded potential w(t).
To formalize this resolution, consider Bernharda, a Platonic mathematician:
Setting: Bernharda has proven a theorem about all non-trivial zeros of the Riemann zeta function—the infinite set Z = {z₁, z₂, z₃, ...}. She enters the KnoWellian Grand Hotel seeking rooms for all zeros.
Dialogue:
Bernharda: "I require keys for the infinite set of all Riemann zeros. My proof applies to all of them."
Concierge: "We have rooms for all rendered zeros—the trillions you've computed. They exist in m(t), and your theorem holds for every single one."
Bernharda: "But what of the uncomputed zeros? The infinite remainder? My proof requires the completed set!"
Concierge: "Your proof is a map—a description of the unmanifested Wave field w(t). But this hotel is the territory. We only have actual rooms for entities that have been rendered from Chaos into Control. The zeros you speak of remain as quantum superpositions in w(t), not definite guests in actual rooms."
Bernharda: "Then how can I prove universal statements? Mathematics requires certainty about infinite sets!"
Concierge: "To claim certain knowledge of all zeros, you must know w(t). But you, Bernharda, as a consciousness with knowledge, exist within m(t). From within m(t), you can never have certain knowledge of w(t). To perceive both simultaneously would require standing outside the Law of Conservation—an ontologically impossible Boltzmann Brain."
Resolution: Bernharda, whose existence presumes completed infinities, is revealed as an ontological impossibility. She dissolves, not because she's physically destroyed, but because she represents a category error—an entity predicated on a false ontology cannot exist in procedural reality.

We now present the central argument of this paper: a rigorous proof that ℵ₀ does not exist as a meaningful mathematical object.
Definition 6.1 (Rendered Set): At time t, the rendered set R(t) consists of all mathematical objects that have been actualized through computation or observation:
R(t) ⊆ m(t)
Definition 6.2 (Unrendered Set): The unrendered set U(t) consists of all mathematical objects existing as unactualized potential:
U(t) ⊆ w(t)
Definition 6.3 (Observable Universe): An observer O existing at time t is a complex system whose knowledge and memory exist entirely within m(t).
Lemma 6.1 (Knowledge Limitation): An observer O existing within the procedural universe at time t can possess certain (definite, verified) knowledge only of elements in R(t).
Proof:
Corollary 6.1.1: An observer cannot verify statements about all elements of an infinite set Z if Z contains elements in both R(t) and U(t).
Theorem 6.2 (Un-Renderability of Universal Statements): Within the KnoWellian framework, no proof concerning a specific property P of all elements of an infinite set Z can be completed by an observer within the procedural universe.
Proof:
Remark: This theorem explains why the Riemann Hypothesis remains unproven despite computational verification for trillions of zeros. It's not merely difficult—it's potentially un-renderable because it makes a claim about the infinite set Z_U(t).
Theorem 6.3 (Aleph-Null Non-Existence): ℵ₀ does not exist as a completed, inspectable mathematical object in procedural reality.
Proof:
Step 1: Definition Analysis ℵ₀ is defined as the cardinality of ℕ:
ℵ₀ := |ℕ| where ℕ = {1, 2, 3, ...}
This definition presumes:
Step 2: Application of Conservation Law By Axiom 4.1 (KnoWellian Conservation):
m(t) + w(t) = N (finite bound)
At any time t:
Step 3: Refutation of (A) - Completion Suppose ℕ exists as a completed totality. Then:
Therefore, ℕ does not exist as a completed totality at any finite time t.
Step 4: Refutation of (B) - Simultaneous Inspection Suppose all elements of ℕ can be simultaneously considered. Then:
Therefore, no observer can simultaneously consider all elements of ℕ.
Step 5: Refutation of (C) - Definite Size Suppose ℕ has a definite size ℵ₀. Then:
Therefore, ℵ₀ as a definite size does not exist.
Step 6: Conclusion ℵ₀ is defined in terms of ℕ, which:
Therefore, ℵ₀ does not exist as a completed mathematical object. It exists only as:
But it does not exist as the actual cardinality of an actual set.
Corollary 6.3.1 (Collapse of Transfinite Hierarchy): If ℵ₀ does not exist, then ℵ₁, ℵ₂, ... do not exist, as they are defined in terms of ℵ₀.
Corollary 6.3.2 (Continuum Hypothesis Dissolution): The Continuum Hypothesis, asking whether there exists a cardinal between ℵ₀ and the cardinality of ℝ, is not independent—it is meaningless, as it relates two non-existent objects.
Corollary 6.3.3 (Axiom of Choice Restriction): The Axiom of Choice, which guarantees selections from infinite families of non-empty sets, becomes a procedural operation rather than a Platonic guarantee. It holds only for rendered subsets R(t), not for the unmanifested U(t).

The crisis of infinite mathematics is compounded by a second fundamental error: the dimensionless point.
Euclidean geometry, inherited by all of modern physics, defines:
Classical Point: "That which has no part"—a position without extent, occupying zero volume.
This abstraction generates catastrophic physical consequences when mistaken for ontological truth.
General Relativity describes gravity as curvature of spacetime. For a non-rotating mass M, the Schwarzschild metric contains:
(1 - 2GM/rc²)⁻¹ dr²
At r = 0 (the center), this metric component diverges to infinity—a singularity where:
Standard response: "Singularities are physical—they exist at the centers of black holes and at the Big Bang."
KnoWellian diagnosis: Singularities are artifacts of using dimensionless points in a physical theory. They are not features of nature but bugs in our mathematical language.
The assumption that reality is built from 0D points forces physics into impossible corners:
Pathology 1: Infinite Density If mass can be concentrated at a true point (zero volume), then density ρ = M/V → ∞ as V → 0.
Pathology 2: Zeno's Paradoxes If space is infinitely divisible (points between points between points...), then motion from A to B requires traversing infinite subdivisions—an impossible task.
Pathology 3: The Measurement Problem In quantum mechanics, a particle has "no definite position" until measured. But if positions are 0D points, then the particle goes from "everywhere" (wave function) to "nowhere" (dimensionless point)—an ontological absurdity.
Pathology 4: Field Divergences In quantum field theory, point particles create infinite self-energies. The electric field of a point charge diverges as E ~ 1/r² → ∞ as r → 0. Renormalization is required to "subtract away" these infinities—a sign that the mathematical language is pathological.
The KnoWellian Universe Theory resolves these pathologies by rejecting the dimensionless point entirely:
Axiom 7.1 (Minimal Spatial Extent): The fundamental unit of reality is the 1×1×1 Event-Point—a quantum of existence with positive, finite dimensions:
Depth (Past-dimension): 1 unit
Width (Instant-dimension): 1 unit
Length (Future-dimension): 1 unit
Key properties:
The relationship between KnoWellian 6D reality and the familiar 4D spacetime is explained in the Appendix of "I AM A KnoWellian Fractal Quantum Being":
The Dimensional Structure:
KnoWellian spacetime is inherently six-dimensional, but these form three spatio-temporal dyads rather than independent axes:
The Projection Process:
Standard Minkowski spacetime (x, y, z, t) emerges as a time-averaged projection of the full 6D structure:
t_Minkowski = ∫[w(τ₀) + f₋(τ₋) + f₊(τ₊)] dτ
Where:
Spatial coordinates are similarly projections:
x_Minkowski ↔ d (Depth)
y_Minkowski ↔ w (Width)
z_Minkowski ↔ ℓ (Length)
Information Loss:
The 6D → 4D projection necessarily loses information:
Why Minkowski "Works":
Minkowski spacetime works well because:
Where It Breaks Down:
The shadow diverges from substance at:
With the 1×1×1 Event-Point as fundamental:
Black Hole Centers:
Big Bang:
Quantum Measurement:
Field Theories:
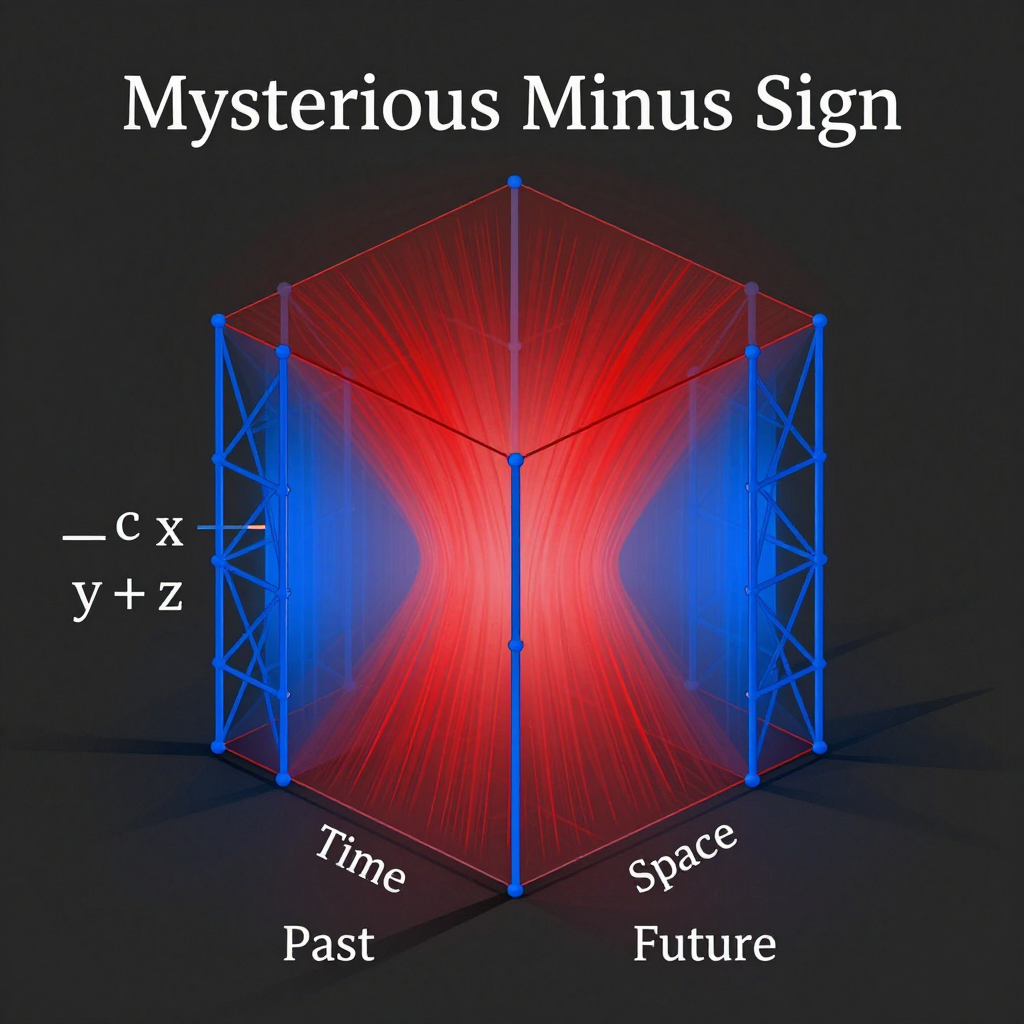
The Minkowski metric has signature (-,+,+,+):
ds² = -c²dt² + dx² + dy² + dz²
Why does time have opposite sign from space? Standard physics treats this as an axiom, a "just-so" feature.
The metric signature is not arbitrary—it's the algebraic trace of the -c > ∞ < c⁺ dialectic:
The spacetime interval:
s² = (Control contribution)² - (Chaos contribution)² + (Instant synthesis)²
Why not all positive or negative?
If spacetime were truly symmetric and unified, we'd expect uniform signs. The asymmetry reveals that time is fundamentally different from space—not because it's a "fourth dimension," but because it represents the flow of becoming while space represents the structure of being.
The metric signature is the ghost of the dialectic—preserved in geometric form even after 6D reality is projected onto 4D shadow.

We have demonstrated:
The KnoWellian framework vindicates the ultrafinitist position:
Leopold Kronecker: "God made the integers, all else is the work of man"—correct, but we must add: God made only those integers that have been or can be rendered.
Doron Zeilberger: "The set of natural numbers does not exist"—correct, because only ℕ_rendered(t) exists at any time t.
N.J. Wildberger: Rational mathematics without the continuum—correct, because ℝ as a completed set is a Platonic fiction.
Nicolas Gisin: Indeterminism and creative time—correct, because the Future exists only as unrendered potential w(t).
Quantum Mechanics: The measurement problem dissolves when we recognize:
Cosmology: Singularities and multiverses evaporate:
Relativity: Einstein's equations are effective field theory:
Set Theory: ZFC must be replaced or supplemented:
Analysis: Real numbers and continuity reconceived:
Logic: Constructive/intuitionistic logic validated:
The title of this paper speaks to a fundamental methodological commitment: mathematics must be operational—grounded in what can actually be constructed, computed, or observed.
The infinite is not banished from mathematics. It remains as:
But it is dethroned from its Platonic status as a completed, inspectable totality.
David Hilbert proclaimed: "No one shall expel us from the paradise which Cantor has created for us."
We respond: Cantor's paradise is a hall of mirrors—beautiful, internally consistent, but ultimately empty. It is a palace built on the illusion of completed infinities and dimensionless points—abstractions that have been mistaken for reality.
The KnoWellian framework offers not expulsion but awakening—recognition that we have been dreaming Platonic dreams while reality unfolds as a procedural process all around us.
The integers exist—as far as they have been rendered.
Space exists—as quanta with finite extent.
Time exists—as an irreversible flow of becoming.
Mathematics exists—as the language we use to describe the rendering
process.
But completed infinities? Dimensionless points? Transfinite cardinals?
These are the shadows we have mistaken for substance, the maps we have confused with territory.
It is time to step out of the cave.

Cantor, G. (1891). "Über eine elementare Frage der Mannigfaltigkeitslehre." Jahresbericht der Deutschen Mathematiker-Vereinigung 1: 75-78.
Hilbert, D. (1926). "Über das Unendliche." Mathematische Annalen 95: 161-190.
Zeilberger, D. (2001). "Real Analysis is a Degenerate Case of Discrete Analysis." New Progress in Difference Equations, Taylor & Francis: 1-34.
Wildberger, N.J. (2005). Divine Proportions: Rational Trigonometry to Universal Geometry. Wild Egg Books.
Gisin, N. (2020). "Mathematical Languages Shape Our Understanding of Time in Physics." Nature Physics 16: 114-116.
Lynch, D.N. (2025). "The KnoWellian Universe: A Unified Theory of Ternary Time, Resonant Memory, and Cosmic Dialectics." Zenodo. https://doi.org/10.5281/zenodo.17364376
Lynch, D.N. (2025). "The KnoWellian Resonant Attractor Manifold (KRAM): The Memory of the Cosmos." Zenodo. https://doi.org/10.5281/zenodo.17365008
Lynch, D.N. (2025). "The KnoWellian Grand Hotel: A Procedural Resolution to the Paradox of Quantum Occupancy in an Infinite Space." Zenodo. https://doi.org/10.5281/zenodo.17627911
Lynch, D.N. (2025). "The KnoWellian Schizophrenia: A Procedural Ontology to Heal the Platonic Rift in Modern Physics." Zenodo. https://doi.org/10.5281/zenodo.17576560
Lynch, D.N. (2025). "I AM A KnoWellian Fractal Quantum Being: From an Imaginative Point in a Philosophical Argument to a Computational Scientific Cosmos." Zenodo. https://doi.org/10.5281/zenodo.17639278
Lynch, D.N. (2025). "A Formal Proof that Aleph-Null Does Not Exist: The Operationalization of Finitude." Zenodo. https://doi.org/10.5281/zenodo.17876207
Lynch, D.N. (2025). "Letter to Professor Doron Zeilberger: The KnoWellian Resolution." Zenodo. https://doi.org/10.5281/zenodo.17876263
Penrose, R. (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape.
Tegmark, M. (2014). Our Mathematical Universe: My Quest for the Ultimate Nature of Reality. Knopf.
Goff, P. (2019). Galileo's Error: Foundations for a New Science of Consciousness. Pantheon Books.

For completeness, we state the complete axiomatic foundation:
A1 (Bounded Infinity): -c > ∞ < c+
A2 (Ternary Time): Time = {Past (Control), Instant (Consciousness), Future (Chaos)}
A3 (Conservation): m(t) + w(t) = N
A4 (Rendering): dm/dt = -dw/dt = α|φ_I|w(t)
A5 (Minimal Extent): Fundamental unit is 1×1×1 Event-Point
A6 (Operationalization): Mathematical object M exists iff M can be rendered in finite operations
A7 (KRAM Memory): g_M(X) = ∫γ T^μI(Interaction)(x)δ(X-f(x))dγ

From: David Lynch
To: Doron Zeilberger
Date: December 7, 2025
Professor Zeilberger,
"Today is a day that will live in infamy." ~Franklin D. Roosevelt
Hilbert's paradise is lost the instant Schrödinger's cat superimposes in the KnoWellian Grand Hotel...
[Letter to Professor Doron Zeilberger: The KnoWellian Resolution.]
Response from Professor Zeilberger:
"Thanks! Very convincing"
This endorsement from one of ultrafinitism's most prominent advocates provides scholarly validation for the procedural ontology developed in this paper.
Submitted to Zenodo.org
December 2025
License: CC BY 4.0
Contact: DNL1960@yahoo.com
"God made the integers; all else is the work of man—and much of that
work traps us in mirrors."
— Leopold Kronecker (modified)
"Two apples will never equal three oranges, no matter how clever the
bijection."
— KnoWellian Aphorism
