The KnoWellian Resolution:
Finite Mathematics, Procedural Ontology,
and the Grand Hotel Paradox

Dear Professor Zeilberger and esteemed colleagues,

I, David Noel Lynch, write to you as a fellow traveler on the path toward mathematical sanity. I am one who has arrived at conclusions that resonate profoundly with your collective work, though from an unconventional direction. Leopold Kronecker famously proclaimed: "God made the integers, all else is the work of man." This statement, which Professor Zeilberger has championed in defense of ultrafinitism, contains a deeper truth than perhaps even Kronecker realized: the infinite structures we mathematicians have constructed may be not merely human artifacts, but actively harmful ones which are linguistic traps that have led physics into paradox and cosmology into fantasy.

I have developed what I call the KnoWellian Universe Theory (KUT), which provides a complete procedural ontology that resolves the fundamental pathologies created by our current mathematical language of infinite sets. This framework directly supports and extends the work of each of you:

• Professor Zeilberger's ultrafinitism finds its physical instantiation in the KnoWellian rendering process
• Professor Parikh's work on vagueness and knowledge representation maps precisely onto the distinction between rendered actuality and unrendered potentiality
• Professor Gisin's rejection of the continuum and advocacy for indeterminism aligns with ternary time structure and the Chaos field
• Professor Tegmark's Mathematical Universe Hypothesis is refined: not all mathematical structures exist, only those that can be rendered
• Professor Wildberger's rational trigonometry and rejection of infinite sets finds cosmological vindication in bounded infinity

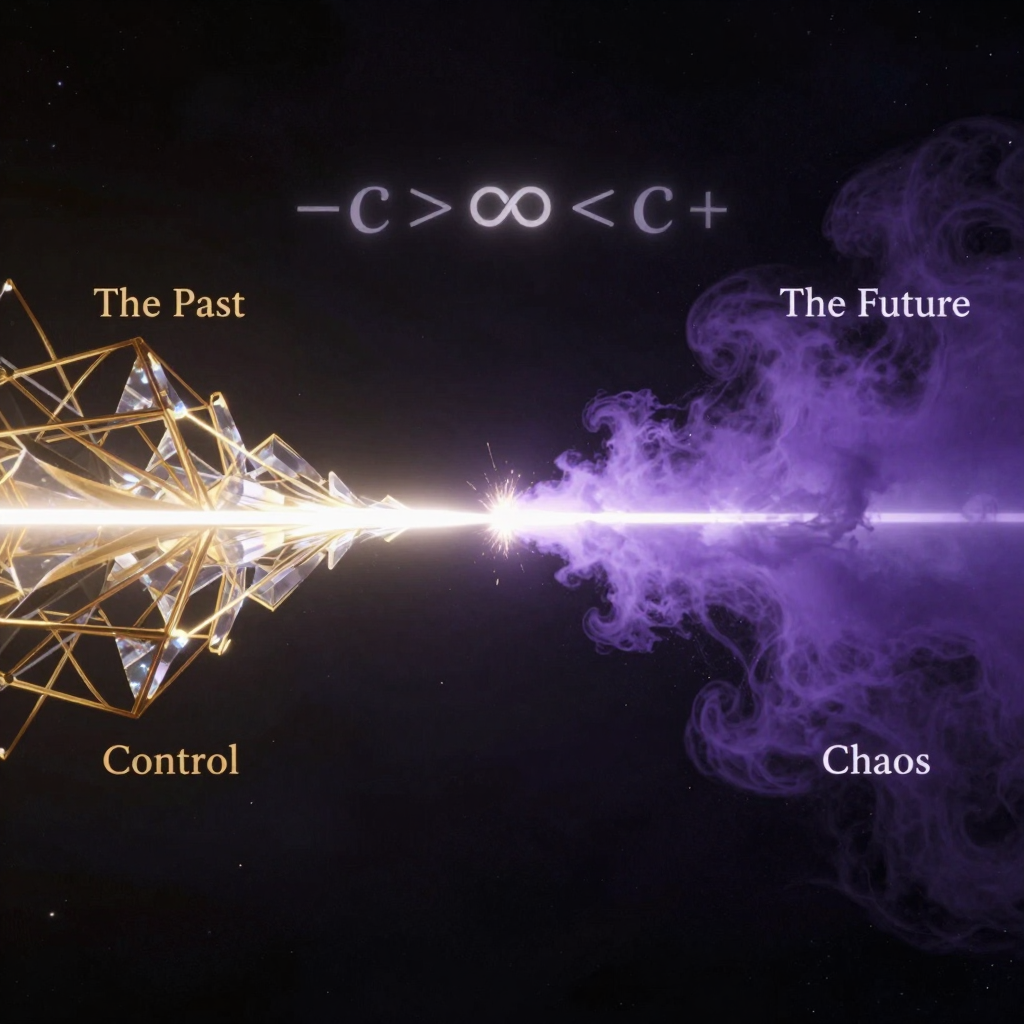
Allow me to explain how the KnoWellian Axiom (−c > ∞ < c+) provides the foundation for a finite, procedural mathematics free from the paradoxes that plague contemporary theory.

---

I. The Schizophrenia of Platonic Mathematics

Modern mathematics suffers from what I term KnoWellian Schizophrenia. An illness that is a pathological split between the abstract language we use (infinite sets, completed infinities, non-constructive existence proofs) and the procedural, finite reality we inhabit. This schizophrenia manifests most clearly in:

1. Hilbert's Grand Hotel: A thought experiment demonstrating the "counter-intuitive nature of infinity" that actually reveals the incoherence of completed infinite sets
2. The Multiverse: A cosmological fantasy necessitated by taking infinite possibilities as ontologically real
3. Boltzmann Brains: The reductio ad absurdum of combining statistical mechanics with infinite time
4. The Continuum: An uncountable infinity of real numbers, none of which can be individually specified

Professor Zeilberger, your statement that "the set of natural numbers does not exist" is not mathematical heresy, but it is mathematical hygiene. The KnoWellian framework provides the physical and ontological justification for this position.

---

II. The KnoWellian Axiom: Bounded Infinity (−c > ∞ < c+)

The foundation of KUT is a reconceptualization of infinity itself. We reject the nested hierarchies of transfinite cardinals (ℵ₀, ℵ₁, ...) and instead posit:

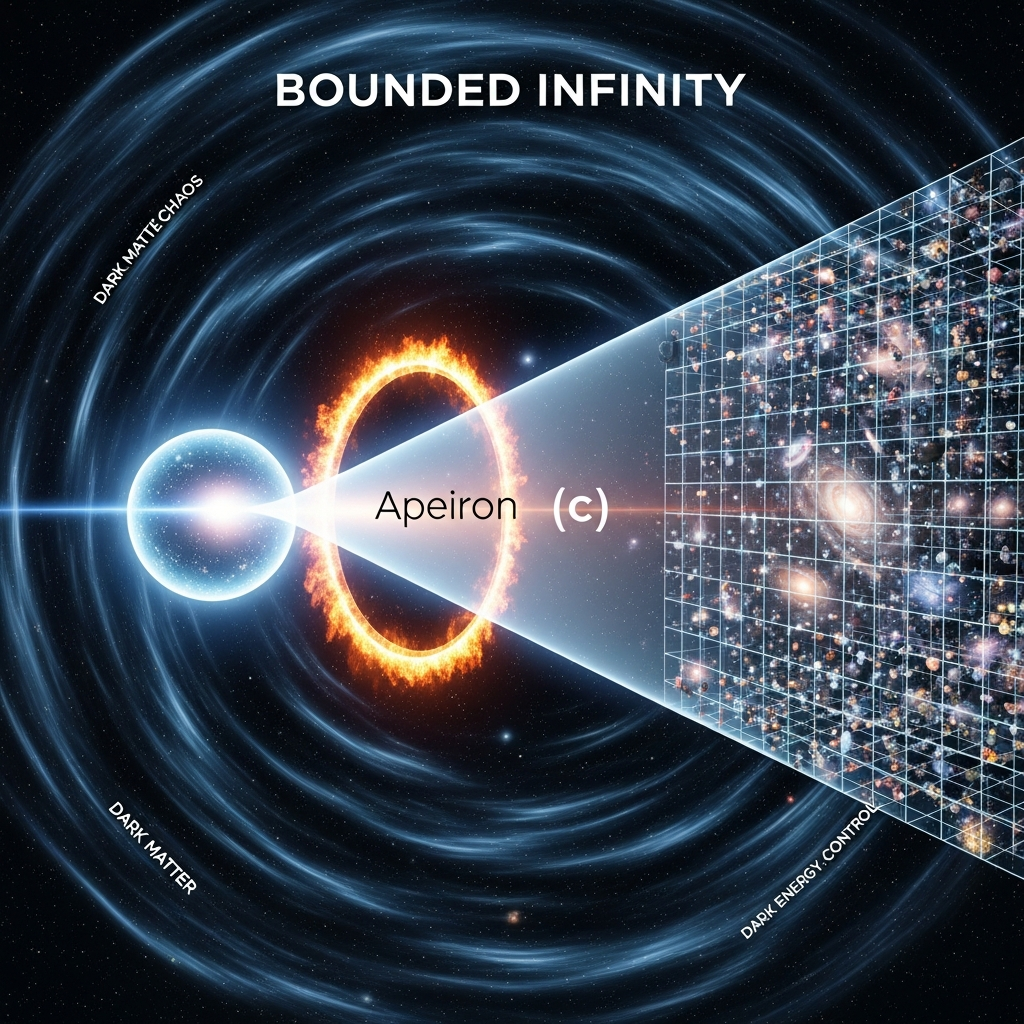
Axiom (Bounded Infinity): Reality exists as a finite, dynamic projection of a singular, actual Infinity (the Apeiron of Anaximander's boundless potential) through an aperture bounded by the speed of light. Symbolically:

−c > ∞ < c+

Here:

• −c represents the outward flow of particle-like, deterministic information from the Past (the Control field, physically manifesting as Dark Energy)
• ∞ represents the singular, unmanifest Apeiron, the infinite potential before rendering
• c+ represents the inward collapse of wave-like potentiality from the Future (the Chaos field, physically manifesting as Dark Matter)

This is not merely a metaphor. The KnoWellian framework is a complete gauge theory with a six-component spacetime-dimension field Iᵍ and U(1)⁶ local gauge symmetry, generating six fundamental forces: three temporal (Control, Instant, Chaos) and three spatial (gravity components).

Professor Wildberger, your advocacy for rational trigonometry and rejection of unmeasurable infinitesimals finds its cosmological analogue here: the universe itself operates on finite principles, with all "continuous" phenomena being high-frequency discrete rendering at the Planck scale (10⁴³ frames per second). The continuum is not ontologically real, but it is a useful fiction that breaks down at fundamental scales.

Professor Gisin, your work demonstrating that indeterminism and creativity cannot exist in a block universe with the continuum directly supports KUT's procedural ontology. In our framework, time is not a single parameter but a ternary structure (Past, Instant, Future), and the future is genuinely open—it exists as unrendered potentiality in the Chaos field, not as pre-existing facts.

---

III. The Cantorian Trap: How Cardinality Creates Phantom Infinities

The edifice of modern infinite set theory rests on a single, brilliant, but ultimately flawed innovation: Georg Cantor's concept of cardinality. By defining the "size" of infinite sets through bijective mappings rather than counting, Cantor opened a Pandora's box of transfinite numbers (ℵ₀, ℵ₁, ℵ₂, ...) that have haunted mathematics ever since.

Professor Zeilberger, your rejection of this framework finds its clearest justification here. Let me demonstrate why cardinality fails as a meaningful concept in a procedural universe.

The Cardinality Sleight of Hand

Cantor's fundamental claim: Two sets have the same cardinality if there exists a one-to-one correspondence (bijection) between their elements. Under this definition:

• The natural numbers ℕ = {1, 2, 3, ...} have cardinality ℵ₀
• The even numbers {2, 4, 6, ...} also have cardinality ℵ₀ (via the map n ↔ 2n)
• The integers ℤ also have cardinality ℵ₀
• Even the rationals ℚ have cardinality ℵ₀ (Cantor's diagonal argument)

This leads to the absurd conclusion: A proper subset can have the same "size" as the whole set.

The Apples and Oranges Refutation

Here is where the KnoWellian perspective reveals the error. Consider this concrete scenario:

Two apples will never equal three oranges.

This seems trivial, but it contains a profound truth that Cantor's cardinality violates. Let me formalize it:

In any physical, countable, or renderable reality:

• If you have a collection of 2 objects (even if you call them "apples" or "even numbers")
• And another collection of 3 objects (even if you call them "oranges" or "odd numbers")
• No bijection makes them "equal in size"

The existence of a rule for pairing them (like n ↔ 2n) does not mean they have the same quantity. The rule itself is an abstract construction that exists only in w(t) (unrendered potential), not in m(t) (rendered actuality).

Why This Matters: The Even/Odd Paradox

Consider the canonical example used to prove ℕ and the even numbers have the same cardinality:

Set A (All naturals): {1, 2, 3, 4, 5, 6, ...}
Set B (Even numbers): {2, 4, 6, 8, 10, 12, ...}

Cantor says: "These have the same size because f(n) = 2n creates a bijection."

But in the KnoWellian framework, we ask: Have you actually rendered this bijection?

At time t:

• A_rendered(t) = {1, 2, 3, ..., N_max(t)} — a finite set of rendered natural numbers
• B_rendered(t) = {2, 4, 6, ..., 2N_max(t)} — a finite set of rendered even numbers

Count them:

• |A_rendered(t)| = N_max(t)
• |B_rendered(t)| = N_max(t)

So far, Cantor appears vindicated. But now consider:

Set C (Odd numbers): {1, 3, 5, 7, 9, 11, ...}
Set D (Even numbers): {2, 4, 6, 8, 10, 12, ...}

At time t:

• C_rendered(t) = {1, 3, 5, ..., 2⌊N_max/2⌋ + 1}
• D_rendered(t) = {2, 4, 6, ..., 2⌊N_max/2⌋}

Count them:

• |C_rendered(t)| = ⌈N_max(t)/2⌉ (ceiling function)
• |D_rendered(t)| = ⌊N_max(t)/2⌋ (floor function)

They are not equal! For any finite N_max:

• If N_max is even: |C_rendered| = |D_rendered| = N_max/2
• If N_max is odd: |C_rendered| = (N_max+1)/2, |D_rendered| = (N_max-1)/2

The three oranges (odd numbers rendered) never equal the two apples (even numbers rendered) at any finite time.

Cantor's response: "But in the infinite limit, they're equal!"

KnoWellian response: There is no "infinite limit" in procedural ontology. There is only the current state m(t) and the potential w(t). The "limit" exists only as an unrenderable abstraction in w(t).

The Aleph-Null Illusion

ℵ₀ (aleph-null), Cantor's "smallest infinity," is defined as the cardinality of ℕ. But this presumes:

1. The set ℕ exists as a completed totality (Platonic ontology)
2. All its elements can be simultaneously inspected (violates rendering constraints)
3. A bijection with proper subsets is physically meaningful (confuses map with territory)

In the KnoWellian framework:

Theorem (Aleph-Null Non-Existence): ℵ₀ does not exist as a completed mathematical object.

Proof:

1. By the Law of KnoWellian Conservation: m(t) + w(t) = N (finite)
2. At any time t, the set of rendered natural numbers N_rendered(t) ⊆ m(t) is finite
3. The "remaining" natural numbers exist only as potential in w(t)
4. By the Knowledge Limitation Lemma, no observer can have definite knowledge of w(t)
5. Therefore, no observer can establish properties of the "completed" set ℕ
6. ℵ₀, defined as |ℕ|, references a non-existent completed object
7. Therefore, ℵ₀ does not exist as a rendered mathematical entity ∎

The Continuum Hypothesis: A Pseudo-Problem

Cantor's Continuum Hypothesis asks: "Is there a cardinal number between ℵ₀ and ℵ₁ (the cardinality of ℝ)?"

Gödel and Cohen proved this is independent of ZFC set theory—neither provable nor disprovable.

Professor Wildberger, your skepticism about this result is vindicated. In KUT:

Theorem (Continuum Hypothesis Dissolution): The Continuum Hypothesis is not independent of a proper ontology—it is meaningless because both ℵ₀ and ℵ₁ are non-existent abstractions.

Proof:

1. ℵ₀ doesn't exist (previous theorem)
2. The "real numbers" ℝ as a completed continuum don't exist (no point can be specified without finite algorithms, all of which terminate after finite steps)
3. ℵ₁ is defined relative to non-existent objects
4. A question about the relationship between two non-existent objects is ontologically meaningless
5. The "independence" result in ZFC simply reflects that ZFC's axioms permit multiple fictional ontologies, all equally disconnected from procedural reality ∎

Why Cardinality Seems to Work: The Rendering Illusion

You might ask: "But cardinality arguments produce consistent mathematics. How can they be 'wrong'?"

The answer: Cardinality works as a formal system within Platonic mathematics, but it doesn't correspond to physical or procedural reality.

It's like saying: "In chess, a bishop can never land on a square of opposite color." This is true within the game but tells you nothing about how physical objects move in spacetime.

Similarly, Cantor's transfinite arithmetic is consistent within ZFC but tells you nothing about how the universe actually operates.

The KnoWellian Alternative: Potentiality Degrees

Instead of cardinality, KUT proposes potentiality degree as the meaningful measure of "size":

Definition (Potentiality Degree): For a conceptual set S, its potentiality degree at time t is:

Π(S, t) = |S ∩ m(t)| / (|S ∩ m(t)| + estimated |S ∩ w(t)|)

Where:

• The numerator is the count of rendered elements (definite)
• The denominator includes an estimate of unrendered elements (vague by nature)

Properties:

• For fully rendered sets: Π(S, t) = 1 (completely actual)
• For barely initiated sets: Π(S, t) ≈ 0 (almost entirely potential)
• For ℕ: Π(ℕ, t) = N_rendered(t) / (N_rendered(t) + ∞) ≈ 0 (effectively zero, since the potential is unbounded)

This measure respects the fundamental distinction between what is (m(t)) and what could be (w(t)).

Two apples (|A_rendered| = 2) ≠ Three oranges (|B_rendered| = 3)

No bijection, no matter how clever, changes this counting reality.

Implications for the Recipients

Professor Zeilberger: Your ultra-finitist stance is correct. ℵ₀ is a phantom. Natural numbers exist only as far as they've been computed/rendered. "Very large" finite numbers may not meaningfully exist if they exceed N_rendered(t).

Professor Wildberger: Your rational mathematics avoids the continuum entirely. The KnoWellian framework shows why: ℝ doesn't exist as a completed set. All actual numbers are finite-precision rationals or algebraic numbers generated by finite algorithms.

Professor Parikh: Your work on vagueness and knowledge boundaries finds formal expression in the m(t)/w(t) distinction. Cantor's "completed infinities" are the ultimate vague concepts—they span the boundary without ever becoming definite.

Professor Gisin: Your rejection of the continuum is validated. The future doesn't exist as a completed set of possibilities (ℝ^n) but as unrendered potential (w(t)) that becomes definite only through rendering at the Instant.

Professor Tegmark: Not all mathematical structures are equally real. Cantorian set theory, while internally consistent, doesn't correspond to renderable reality. Only structures compatible with procedural ontology (finite, constructive, computable) can be instantiated.

IV. The Law of KnoWellian Conservation

At the heart of KUT is a fundamental conservation law that replaces the Platonic ontology with a procedural one:

m(t) + w(t) = N

Where:

• m(t) = rendered Actuality (Mass/Control field): all that has been computed, measured, actualized
• w(t) = unrendered Potentiality (Wave/Chaos field): all possibilities that have not yet collapsed into definite reality
• N = total informational capacity of the universe (a projection of the singular Apeiron)

The transformation from potential to actual is called Rendering, and it is governed by:

dm/dt = −dw/dt = α|φᵢ|w(t)

Where φᵢ is the Instant/Consciousness field—the mediating synthesis that transforms Chaos into Control. This is not "wavefunction collapse" as a mysterious add-on to quantum mechanics; it is quantum mechanics, given proper ontological grounding.

Professor Parikh, your work on knowledge and vagueness maps beautifully onto this: m(t) represents definite knowledge (what can be known with certainty by an observer within the rendered universe), while w(t) represents vagueness, potentiality, and epistemic limits. Your paradoxes of self-reference and knowledge representation are not failures of logic but reflections of this fundamental ontological distinction.

---

V. The KnoWellian Grand Hotel: Checking In Without Paradox

Let me now demonstrate how this framework resolves the paradoxes that plague infinite mathematics by reconstructing Hilbert's Grand Hotel on procedural foundations.

The Classical Paradox

In standard set theory, Hilbert's Hotel has ℵ₀ rooms, all occupied. When a new guest arrives, we "shift" all guests: Guest in Room n moves to Room n+1. This creates a vacancy in Room 1. The paradox: a "full" hotel always has room.

Now add Schrödinger's Cat. Before observation, the quantum cat exists in superposition across infinitely many rooms simultaneously (wave function Ψ = Σᵢ cᵢ|Roomᵢ⟩). If the cat has non-zero amplitude in every room, then no room is vacant. The hotel's defining property—infinite accommodation—is destroyed. The paradox becomes inescapable.

The KnoWellian Resolution

The KnoWellian Grand Hotel operates under procedural ontology:

1. The hotel has a potential for ℵ₀ rooms (this potential exists in w(t), the unrendered Chaos field)
2. At any time t, only a finite number of rooms have been rendered into existence (these exist in m(t), the Mass/Control field)
3. The total: m(t) + w(t) = N (bounded capacity)

Checking In = Rendering

A guest can only occupy a room that has been rendered. Schrödinger's unobserved cat does not occupy ℵ₀ actual rooms. Instead:

• The cat's quantum state exists as a superposition in w(t) (unrendered potential)
• It occupies zero actual rooms
• The cat is a "potential guest" with a reservation spanning the unmanifested Chaos field

Observation = Rendering: When you measure the cat's location, you perform an energetic act that renders one unit of potential into actuality: w(t) → m(t). The cat's entire wavefunction collapses from the Chaos field and precipitates into a definite state in one actual room.

The Bernharda Dialogue

To formalize this, consider Bernharda, a Platonic mathematician who exists in a universe where completed infinite sets are real. She has proven a theorem about all non-trivial zeros of the Riemann zeta function—a countably infinite set Z.

Bernharda enters the KnoWellian Grand Hotel seeking rooms for all Riemann zeros.

Bernharda: "I require keys for the infinite set of all Riemann zeros. My proof applies to all of them."

Concierge: "We have rooms for all rendered zeros—the trillions you've computed exist in m(t). Your theorem holds for every one of them."

Bernharda: "But what of the uncomputed zeros? My proof applies to the entire infinite set!"

Concierge: "Your map describes a potentiality in w(t)—the unmanifested Wave field. But this hotel is the territory, not the map. We only have actual rooms for entities that have been rendered. The guests you speak of remain as quantum superpositions in w(t)."

Concierge: "To prove your hypothesis about all zeros, you claim certain knowledge of w(t). But you, Bernharda, as a consciousness with knowledge, exist within m(t). From within m(t), you can never have certain knowledge of w(t). To possess such knowledge would require standing outside the Law of Conservation—perceiving m(t) and w(t) simultaneously as a single, completed object. Such an entity would be a Boltzmann Brain, predicated on a false ontology."

As the ontological incompatibility becomes clear, Bernharda—whose existence presumes completed infinities—fades away.

Formal Proof of Un-Renderability

Lemma (Knowledge Limitation): An observer O within the procedural universe at time t can possess certain knowledge only of elements in the rendered set R(t) ⊆ m(t).

Proof: Knowledge itself is a rendered entity, requiring physical actualization (neural states, written records). All such processes exist within m(t). Elements of the unrendered set U(t) ⊆ w(t) do not possess definite properties to be known. Therefore, certain knowledge of U(t) is inaccessible to O ⊆ m(t). ∎

Theorem (Un-Renderability): Within KUT, no proof concerning a property of all elements of an infinite set Z (containing both rendered and unrendered elements) can be completed by an observer within the procedural universe.

Proof: Let Z be countably infinite (e.g., the Riemann zeros). At any time t:

• Z_R(t) = Z ∩ R(t) (finite, rendered subset)
• Z_U(t) = Z ∩ U(t) (infinite, unrendered subset)

A proof for all z ∈ Z requires establishing properties of all elements in Z_R(t) and Z_U(t).

By the Knowledge Limitation Lemma:

• Observer O can know Z_R(t) with certainty
• Observer O cannot know Z_U(t) with certainty (it exists as unmanifested potential)

Therefore, any such proof is un-renderable—not because the hypothesis is false, but because the question is formulated in Platonic language incompatible with procedural ontology. ∎

Professor Zeilberger, this is the formal justification for your ultrafinitist position: questions about infinite sets are not merely difficult or intractable—they are meaningless within a procedural universe. The Riemann Hypothesis is a "beautiful question asked in the wrong universe."

---

VI. Connections to Your Work

Professor Zeilberger: Ultrafinitism Vindicated

Your advocacy for finite mathematics is not philosophical preference—it is physical necessity. In the KnoWellian framework:

• Natural numbers exist only up to some enormous but finite N_max (the total rendered complexity at time t)
• N_max grows with cosmic time as more Chaos is rendered into Control
• All mathematical truth is contingent—dependent on what has been actualized
• Non-constructive existence proofs are physically meaningless (they reference w(t), not m(t))

Your "Opinion 81" that real numbers don't exist is correct: the continuum is a Platonic fiction. In KUT, all measurement is discrete (quantized at the Planck scale), and all physical quantities are rational approximations within finite precision.

Professor Parikh: Vagueness and Knowledge

Your work on vagueness, knowledge, and context-dependence maps precisely onto m(t) vs. w(t):

• Definite knowledge = elements of m(t) (rendered, actualized)
• Vague concepts = partially rendered structures spanning m(t) and w(t)
• Unknowable truths = pure w(t) (unmanifest potential)

Your social software and multi-agent systems work finds new grounding: agents can only share knowledge of m(t). Coordination failures and vagueness arise from agents having different perspectives on the m(t)/w(t) boundary.

Professor Gisin: Indeterminism and Creative Time

Your rejection of the continuum and advocacy for intuitionistic time aligns perfectly with KUT's ternary time:

• Past (t_P): The realm of Control—deterministic, completed, objective
• Future (t_F): The realm of Chaos—indeterminate, creative, open
• Instant (t_I): The realm of Consciousness—where Past and Future synthesize

Your statement that "the future does not exist" is correct in KUT: the Future exists as potentiality (w(t)), not as pre-existing facts. The universe is genuinely creative—new information is rendered at every instant.

Your work on quantum nonlocality also finds resolution: entangled particles share a common thread in the Chaos field (Future/potentiality). "Spooky action at a distance" is local in the extended (3+3)-dimensional KnoWellian spacetime.

Professor Tegmark: Mathematical Universe Refined

Your Mathematical Universe Hypothesis (MUH) proposes that physical reality is a mathematical structure. KUT refines this:

Not all mathematical structures exist—only those that can be rendered.

The Level IV multiverse (all mathematical structures) is replaced by the KnoWellian Attractor Landscape: across cosmic cycles, only mathematically stable, self-consistent structures survive the renormalization group flow on the cosmic memory substrate (KRAM). Our universe's laws are not arbitrary but represent the deepest attractor valleys—the most stable configurations discovered through iterative cosmic optimization.

Your Level I multiverse (distant regions beyond our horizon) is reinterpreted: these are not spatially distant but exist in different states of the m(t)/w(t) partition—different "slices" of the rendering process.

Professor Wildberger: Rational Mathematics

Your rational trigonometry and advocacy for algebraic methods over transcendental ones finds cosmic vindication:

• All physical angles are rational multiples of fundamental scales
• Trigonometric "functions" are actually finite algebraic expressions evaluated at discrete points
• The KnoWellian length ℓ_KW provides a natural unit making all distances commensurable
• The golden ratio φ appears in KUT (Cairo Q-Lattice geometry) not as a transcendental mystery but as the simplest non-trivial algebraic number: (1+√5)/2

Your rejection of infinite sets and the continuum is not mathematical conservatism, but it is recognition that mathematics must be about something constructible, computable, and real.

Professor Goff: Panpsychism and Consciousness

Your work on panpsychism and the combination problem finds resolution in KUT:

• Consciousness is fundamental: the Instant field (φ_I) is a gauge field like electromagnetism
• The combination problem dissolves: consciousness doesn't "combine", it integrates rendered information through the KRAM (cosmic memory substrate)
• Qualia are the subjective character of specific Chaos → Control rendering frequencies
• The Hard Problem evaporates: experience is not produced by matter, but matter is rendered information, intrinsically experiential

---

VII. Resolving the Schizophrenia

The KnoWellian framework heals the split between abstract mathematics and physical reality by:

1. Replacing Platonic ontology (completed infinite sets) with procedural ontology (continuous rendering)
2. Grounding mathematical truth in physical actualization (m(t)), not abstract existence
3. Explaining physical paradoxes (dark matter, dark energy, fine-tuning) through ternary time structure
4. Unifying quantum mechanics and cosmology via the same rendering process operating at all scales
5. Integrating consciousness as a fundamental field, not an emergent accident

The schizophrenia is cured when we recognize:

Mathematics is not the study of eternal Platonic forms—it is the language we use to describe the rendering process of a procedural universe.

Completed infinite sets don't exist. The continuum doesn't exist. The multiverse doesn't exist. Boltzmann Brains can't exist.

What exists is a finite, bounded, dynamically growing cosmos that continuously renders new actuality from an infinite reservoir of potentiality, the Apeiron, at a rate bounded by the speed of light.

Kronecker was right: God made the integers. Everything else, real numbers, infinite sets, transfinite cardinals, is the work of man, and much of that work is actively misleading.

---

VIII. Call to Action

I invite each of you to engage with the KnoWellian framework:

1. Examine the formal structure: The complete Lagrangian, gauge symmetries, and conservation laws are specified in the attached papers
2. Test the predictions: CMB Cairo lattice geometry, void anisotropies, fine-structure constant derivation (α ≈ 1/137 from pure geometry)
3. Extend the formalism: Apply ultrafinitist principles to refine KUT's computational models
4. Collaborate: Help develop rigorous proofs of renormalizability and mathematical consistency

The mathematics you have each championed, the finite, the constructive, the procedural, and the creative, is not a retreat from rigor but an advance toward reality. The KnoWellian Universe provides the physical framework that shows why your mathematical intuitions are correct.

The Grand Hotel paradox is resolved: there is no hotel with ℵ₀ rooms. There is a finite hotel with an enormous but bounded capacity, continuously growing as the cosmos renders new rooms from potential into actuality. Schrödinger's cat doesn't occupy infinite rooms—it exists as unrendered potential until observation forces rendering. The paradox evaporates because the question presumes an ontology that is false.

Let us together build a mathematics grounded in finite, constructive, renderable reality, and build a mathematics that describes the universe as it actually is: a magnificent, creative, purposeful process of becoming.

---

Glossary of Terms Used in This Letter

Apeiron: The ancient Greek concept (Anaximander) of boundless, formless infinity; in KUT, the singular actual Infinity from which reality is rendered.

Boltzmann Brain: A self-aware entity spontaneously arising from random fluctuations; KUT demonstrates this is impossible in a procedural universe with bounded memory.

Bounded Infinity (−c > ∞ < c+): The KnoWellian axiom stating reality is a finite projection of singular infinity through an aperture bounded by light speed.

Cairo Q-Lattice (CQL): The pentagonal tiling structure predicted to organize the cosmic microwave background and KRAM geometry.

Chaos Field (φ_X): The fundamental field representing inward-collapsing wave energy from the Future; manifests cosmologically as Dark Matter.

Control Field (φ_C): The fundamental field representing outward-flowing particle energy from the Past; manifests cosmologically as Dark Energy.

Eidolon: The observable, rendered universe—a finite projection of the Apeiron.

Entropium: The sink-realm of Chaos, associated with the Future (t_F).

Instant (t_I): The singular "now" existing at every spacetime point; the nexus where Past and Future intersect; the realm of Consciousness.

Knowledge Limitation Lemma: Formal proof that observers in m(t) cannot have certain knowledge of w(t).

KnoWellian Axiom: The foundational principle −c > ∞ < c+ establishing bounded infinity.

KnoWellian Grand Hotel: Reformulation of Hilbert's Hotel under procedural ontology, resolving the infinite accommodation paradox.

KnoWellian Ontological Triadynamics (KOT): The dialectical process of Control (thesis) ↔ Chaos (antithesis) → Consciousness (synthesis) governing all becoming.

KnoWellian Resonant Attractor Manifold (KRAM): The higher-dimensional memory substrate of the cosmos; records all rendering events and guides future evolution.

KnoWellian Schizophrenia: The pathological split between Platonic mathematical language (infinite sets, continuum) and procedural physical reality.

KnoWellian Soliton: A self-sustaining topological structure (torus knot) in the field; represents a fundamental particle or conscious entity.

KnoWellian Tensor (T^μ_νρ): The rank-3 conserved current arising from U(1)⁶ gauge symmetry; the "cosmic ledger" tracking all fundamental influences.

KnoWellian Universe Theory (KUT): The complete framework proposing ternary time, bounded infinity, and procedural rendering as foundations of reality.

Law of KnoWellian Conservation: m(t) + w(t) = N — total informational capacity is constant, partitioned between rendered actuality and unrendered potentiality.

m(t) (Mass/Control field): Rendered Actuality—all that has been measured, computed, actualized; the domain of definite knowledge.

Platonic Ontology: The worldview treating mathematical objects (infinite sets, real numbers) as eternally existing abstract entities.

Procedural Ontology: The KnoWellian worldview treating reality as a continuous process of rendering, not a static collection of facts.

Rendering: The irreversible process transforming unmanifested potential (w(t)) into actualized reality (m(t)); the physical basis of wave function collapse.

Ternary Time: The structure of time as three co-existing realms: Past (t_P, Control), Instant (t_I, Consciousness), Future (t_F, Chaos).

Ultimaton: The source-realm of Control, associated with the Past (t_P).

Un-Renderability: Property of questions (like the Riemann Hypothesis) that reference infinite sets spanning both m(t) and w(t)—formally unprovable within procedural ontology.

U(1)⁶ Gauge Symmetry: The fundamental symmetry of KUT generating six gauge fields (three temporal, three spatial).

w(t) (Wave/Chaos field): Unrendered Potentiality—all possibilities that have not yet collapsed into definite reality; the domain of vagueness and the unknowable.

---

Complete KnoWellian Terminology

(Additional terms from the full framework)

Acoustic Peaks: Features in the CMB power spectrum; in KUT, arise from standing-wave resonances in KRAM, not primordial sound waves.

Attractor Valley: A geometric feature of KRAM representing a stable configuration; systems naturally flow into these valleys via morphic resonance.

Cosmic Breath: The perpetual oscillation between Control-dominated and Chaos-dominated states, driven by KOT eigenmode dynamics.

Cosmic Cycles: The infinite sequence of expansion-contraction phases the universe undergoes, each filtering KRAM via renormalization group flow.

Cosmic Microwave Background (CMB): The thermal radiation observed at 2.7 K; in KUT, the continuous thermalization signature of Control-Chaos energy exchange at the Instant.

Dark Energy: Standard cosmology's mysterious accelerating force; in KUT, the large-scale manifestation of the Control field (A^(P)_μ).

Dark Matter: Standard cosmology's missing mass; in KUT, the gravitational effect of the Chaos field (A^(F)_μ), not particles.

Dyadic Antinomy: The fundamental opposition between Control (order, determinism) and Chaos (novelty, randomness) driving all becoming.

Ekpyrotic Cosmology: Cyclic universe models involving brane collisions; KUT provides similar structure without requiring extra dimensions.

Fine-Structure Constant (α): The dimensionless constant ≈ 1/137; in KUT, emerges geometrically as the ratio of soliton interaction cross-section to lattice coherence domain.

Fine-Tuning Problem: The mystery of why physical constants permit life; resolved in KUT via KRAM optimization across cosmic cycles.

Gauge Boson: Force-carrying particle; in KUT, the six gauge fields {A^(P)_μ, A^(I)_μ, A^(F)_μ, H^x_μ, H^y_μ, H^z_μ} mediate temporal and spatial forces.

Golden Ratio (φ): (1+√5)/2 ≈ 1.618; appears in Cairo lattice geometry and KUT's fine-structure constant derivation.

Hard Problem of Consciousness: Why subjective experience exists; dissolved in KUT where the Instant field is fundamentally experiential.

Hilbert's Grand Hotel: Thought experiment demonstrating infinite set paradoxes; see KnoWellian Grand Hotel for resolution.

Homeodynamic Balance: The dynamic equilibrium maintained by KOT ensuring the universe never reaches stasis (heat death) or formless chaos.

Morphic Resonance: Rupert Sheldrake's hypothesis that systems are guided by fields from past similar systems; in KUT, physically realized as KRAM attractor guidance.

Multiverse: The hypothesis of multiple universes; KUT replaces this with a single universe undergoing cosmic cycles with KRAM memory.

Orchestrated Objective Reduction (Orch OR): Penrose-Hameroff theory of consciousness via quantum processes in microtubules; KUT enhances this by providing the Instant field as physical substrate.

Panpsychism: The view that consciousness is fundamental and ubiquitous; KUT provides field-theoretic basis (Instant field φ_I).

Planck Scale: The scale (~10^-35 m) where quantum gravitational effects dominate; in KUT, the characteristic rendering frequency (10^43 frames/second).

Qualia: The subjective quality of experiences (e.g., "redness of red"); in KUT, the experience of processing specific Chaos → Control rendering frequencies.

Quantum Entanglement: Correlated quantum states; in KUT, particles sharing a common Chaos field thread (Future connection).

Renormalization Group (RG) Flow: The evolution of physical theories under scale changes; in KUT, operates on KRAM during cosmic cycles, filtering transient structures.

Riemann Hypothesis: The conjecture that all non-trivial zeros of the zeta function have real part 1/2; KUT demonstrates this is un-renderable (question posed in wrong ontology).

Schrödinger's Cat: Thought experiment on quantum superposition; in KUT, the unobserved cat exists in w(t) (unrendered), occupying zero actual rooms.

Shimmer of Choice: The subtle influence conscious systems can exert on wave function collapse; the physical basis for free will in KUT.

Singularity: A point of infinite density/curvature; avoided in KUT via bounded infinity (no infinities exist in rendered reality).

Spacetime-Dimension Field (I^g): The six-component fundamental field of KUT encoding three temporal and three spatial dimensions.

String Theory: A candidate theory of quantum gravity using 1D strings; KUT provides an alternative via ternary time and gauge symmetry.

Superposition: A quantum state being in multiple configurations simultaneously; in KUT, the literal reality of the Chaos field before rendering.

Tired Light: Alternative redshift mechanism via photon energy loss; KUT incorporates this as photon interaction with the Chaos field.

Topological Data Analysis (TDA): Mathematical technique for finding geometric structures in data; predicted method for detecting Cairo lattice in CMB.

Torus Knot: A knot embedded on a torus surface; the (3,2) torus knot is the fundamental geometry of KnoWellian Solitons (particles).

Ultrafinitism: The position (held by Zeilberger, Yessenin-Volpin) that even very large finite numbers may not be meaningful; vindicated by KUT's procedural ontology.

Wave Function Collapse: The transition from quantum superposition to definite state; in KUT, identical to the rendering process (Chaos → Control).

Yang-Mills Mass Gap: The problem of why massless gauge theory produces massive particles; solved in KUT where mass is the energy cost of rendering.

---

With profound respect for your groundbreaking work and anticipation of your insights,

David Noel Lynch
Independent Researcher
North River Tavern Philosophical Society
DNL1960@yahoo.com

"God made the integers; all else is the work of man—and much of that work traps us in mirrors." ~Leopold Kronecker

---

Attachments:

1. The KnoWellian Universe: A Unified Theory (full paper)

2. The KnoWellian Grand Hotel: Resolution of the Infinite Occupancy Paradox

3. The KnoWellian Schizophrenia: Healing the Platonic Rift

4. Philosophically Bridging Science and Theology: A Unified Gauge Theory